

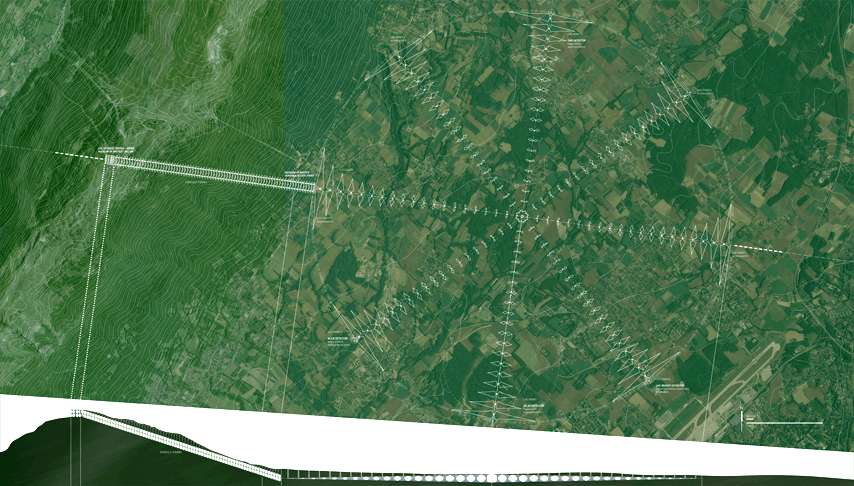
The Large Hadron Collider (LHC) in Geneva, Switzerland is the world's largest scientific experiment, but operates on two opposite scales. In order to investigate the subatomic, the machine needs to exists at the scale of a city, to achieve the required power to reach the scale of the atom. It is a particle collider - a perfectly circular tube that smashes electrons head-on with one another in tiny explosions, three hundred feet underground with a diameter of almost six miles: the distance from Battery Park to the Upper East Side of Manhattan.
The charge for this options studio project is to create a completely fantastic space for the LHC, one that attempts to deal with this contrast in scales within the collider. The space within the ring, and a mountaintop next to it, is the site for this project. A simple set of geometric constraints is deployed to carve out space - the intersections and interactions between simple right cones. The cone deals with two opposite scales as well - it condenses to a single discrete point, but left unconstrained, it extends to the infinite. To curtail this extension, the cones are intersected and trimmed with each other in systematic ways. Since cones contain both a right angle and circular geometries within them, some intersections create simple, square shapes that can link up with other normal objects, while some intersections create predictable geometric shapes like parabolas, and others create unpredictible figural space curves. These intersections are categorized to create a catalogue of caverns, columns, bridges, staircases, flat planes and sculptural forms that are all derived from a single geometric foundation.
The earthen interior of the collider ring is hollowed out using conic intersections that create huge columns and caverns, and the interior becomes a large lake from groundwater. The ring sits next to a mountain range - a set of conic intersections that create stone bridges and skylights is used to carve a diagonal tunnel though this mountain, supporting an underground gondola line extending from the ring to the summit. At the summit, the mountain is hollowed out using conic intersections that create flat planes and interior rooms to become a sort of sublime gallery. While mentally inhabiting the cavernous spaces or viewing the sculptural figures, one becomes aware that every space and solid is created from the same geometric interaction. Whether realistic or not, spatial complexity need not come from complicated formulas or parametric scripts - it can be achieved through regular, thoughtful and considered systems.